相控阵天线波束图样（第二部分）：栅瓣与波束偏频

Part 2: Grating Lobes and Beam Squint

引言

这是我们关于相控阵天线方向图三部分系列文章中的第二篇。在第一部分中，我们介绍了相控阵的波束指向概念，并探讨了影响阵列增益的因素。在第二部分中，我们将讨论栅瓣（Grating Lobes）和波束偏频（Beam Squint）。

栅瓣可能不容易直观理解，因此我们将借用其与数字转换器中信号混叠（aliasing）的相似性，并据此将栅瓣视为一种空间混叠。接着，我们将探讨波束偏频问题。波束偏频是指当我们使用相位移而不是真实时间延迟来实现波束指向时，天线方向图在频率范围内发生的“失焦”现象。

我们还将讨论这两种波束指向方式之间的权衡，并了解波束偏频对典型系统性能的影响。

栅瓣简介

到目前为止，我们只讨论了阵元间距为 d = λ/2 的情况。图 1 开始说明为什么 λ/2 的阵元间距在相控阵中如此常见。

图中展示了两种情况。首先是蓝色曲线，重复了第一部分图 11 中的 30° 波束图。接着，将 d/λ 的间距增加到 0.7，以展示天线方向图的变化。

随着间距的增加，可以看到波束宽度减小，这是一个积极结果。波束零点之间的间距减小，使它们更靠近，这也是可以接受的结果。

但现在在另一个角度（此处为 –70°）出现了一个全阵列增益的次波束，这是一个非常不利的结果。这个天线增益的“副本”被定义为栅瓣（grating lobe），可以视为一种空间混叠（spatial aliasing）。

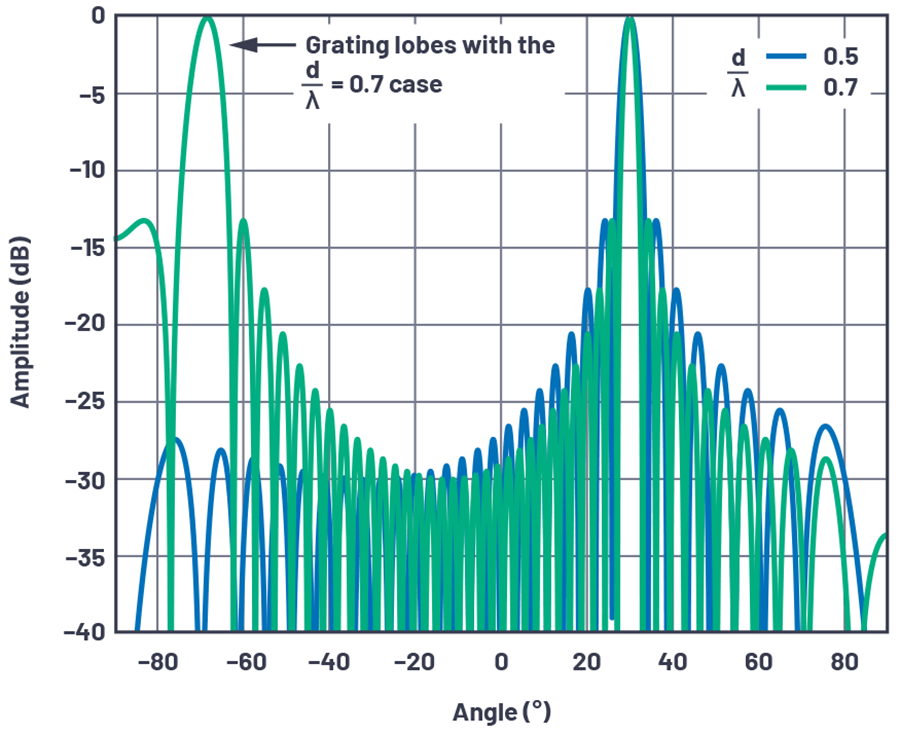
图 1. 一个 32 阵元线性阵列在两种不同 d/λ 间距下的归一化阵列因子。

与采样系统的类比

为了更直观地理解栅瓣，可以将其类比为采样系统中的混叠现象。在模数转换器（ADC）中，欠采样常用于接收机架构的频率规划中。欠采样是指有意降低采样率 f_S，使得采样过程将高于f_S/2 的频率（即高奈奎斯特带）转换为出现在第一个奈奎斯特带中的混叠信号。这将导致高频信号在 ADC 输出中表现为较低频率的信号。

在相控阵中也存在类似的类比关系，其中天线阵元对波前进行空间采样。如果我们认为每个波长需要两个采样点（即两个阵元）才能避免混叠，那么奈奎斯特采样定理就可以推广到空间域。

因此，如果阵元间距大于 λ/2 ，就可以将这种现象视为空间混叠（spatial aliasing）。

栅瓣出现的位置如何计算

那么，这些空间混叠（即栅瓣）会出现在什么位置呢？在第一部分中，我们展示了跨阵列施加相位移与波束角之间的关系。

反过来，我们也可以将波束角表示为相位移的函数：

arcsin 函数仅在其自变量介于 –1 到 +1 之间时才会产生实数解。超出这个范围，解将不是实数——这在电子表格软件中表现为常见的 “#NUM!” 错误。

还需注意，公式（2）中的相位具有周期性，每隔 2π 重复一次。因此，我们可以将∆Φ 替换为 (m × 2π + ∆Φ) ，从而得到波束指向的扩展表达式：

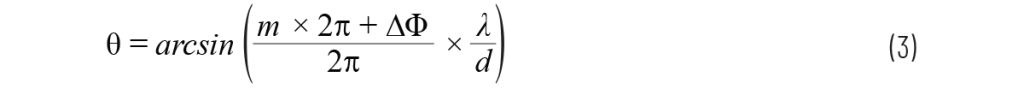
其中 m=0,±1,±2,…m = 0, ±1, ±2, …

为了避免栅瓣，我们的目标是仅获得一个实数解。在数学上，这可以通过保持以下条件来实现：

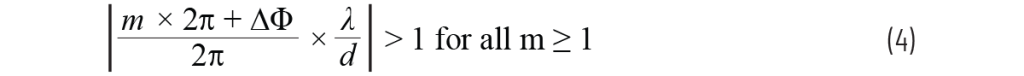
如果满足这一条件，那么所有空间镜像项（即 m=±1,±2,m = ±1, ±2, 等）将导致 arcsin 无实数解，我们就可以忽略它们。

但如果无法满足这一条件，从而使某些 m>0 的值导致 arcsin 产生实数解，则会出现多个解：即栅瓣。

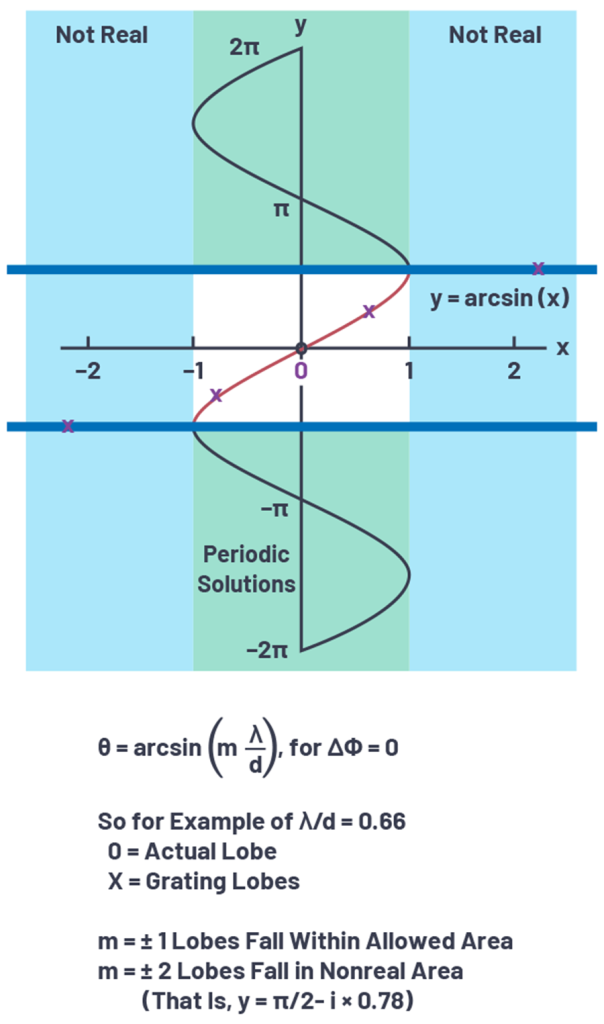
图 2. 将 arcsin 函数应用于栅瓣的计算。

当 d > λ 且 θ = 0° 时的栅瓣

让我们通过一些示例来更清楚地说明这一点。首先，考虑机械波束零向的情况，即 θ = 0，因此 ∆Φ = 0。那么，公式（3）可简化为：

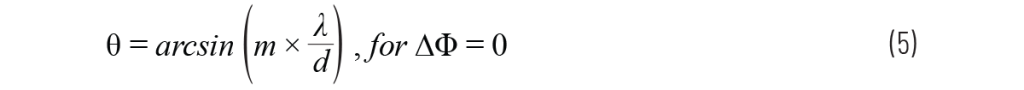
根据这个简化公式，如果 λ/d > 1，则只有当 m = 0 时，自变量才会落在 –1 到 +1 的范围内。而此时自变量为 0，arcsin(0) = 0°，即机械波束零向角。这一结果完全符合预期。

此外，对于任意 m ≥ 1，arcsin 的自变量将大于 1，从而无实数解。因此，当 θ = 0 且 d < λ 时，将不会出现栅瓣！

然而，如果 d > λ（即 λ/d < 1），则可能存在多个解，也就可能出现栅瓣。例如，当 λ/d = 0.66（即 d = 1.5λ）时，arcsin 函数将在 m = 0 和 m = ±1 时有实数解。

其中，m = ±1 表示第二个解，即期望信号的空间混叠。因此，我们预期将看到三个主瓣，且幅度大致相等，分别位于：

• arcsin(0 × 0.66)
• arcsin(1 × 0.66)
• arcsin(–1 × 0.66)

换算成角度分别是 0° 和 ±41.3°。

事实上，图 3 中的阵列因子图正好展示了这一结果。

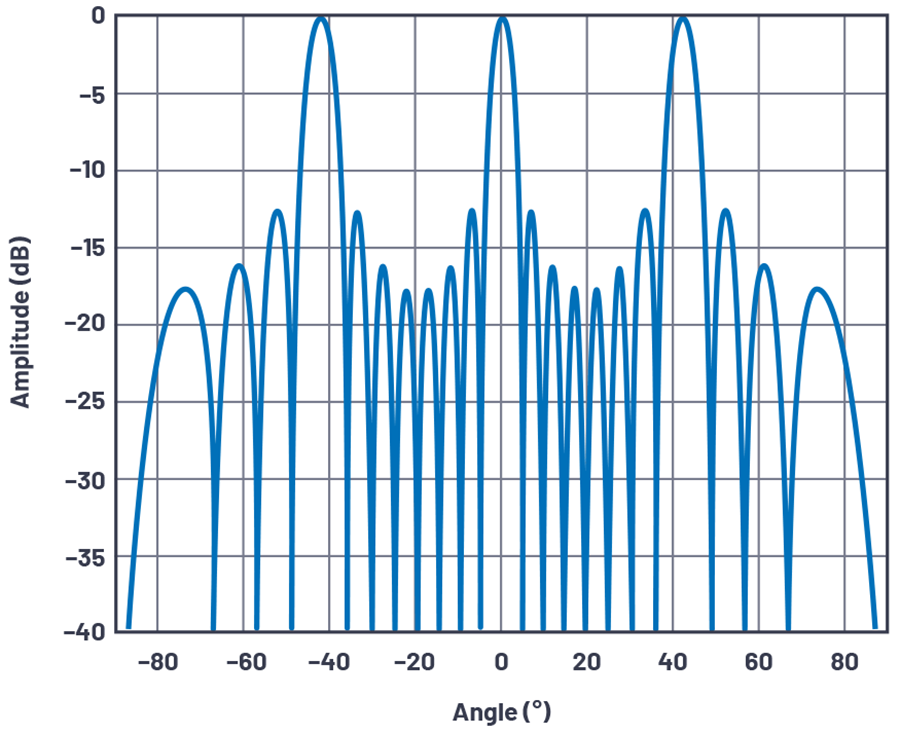
图 3. 阵列因子在波束零向下的分布（d/λ = 1.5，N = 8）

当 λ/2 < d < λ 时的栅瓣

在简化栅瓣公式（公式 5）时，我们选择只关注机械波束零向（∆Φ = 0）的情况。我们已经看到，在机械波束零向，若 d < λ，则不会出现栅瓣。但根据采样理论的类比，我们也知道，只要阵元间距大于 λ/2，就有可能出现某种形式的栅瓣。那么，当 λ/2 < d < λ 时，栅瓣会出现在什么位置？

首先，回忆第一部分图 4 中，相位与波束指向角之间的变化关系。我们看到当主瓣偏离机械波束零向时，∆Φ 的范围为：

∆Φ 从 0 到 ±π

因此，

的范围是：

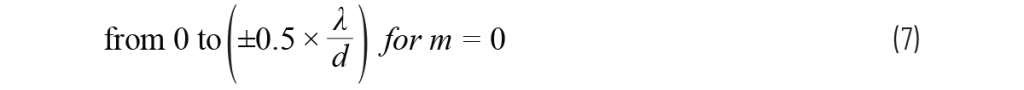
而对于 |m| ≥ 1，其结果总是大于：

如果我们希望对所有 |m| ≥ 1 的情形下，arcsin 函数的自变量始终大于 1，从而无实数解，则这将限制 λ/d 的最小允许值。

考虑以下两种情况：

• 如果 λ/d ≥ 2（即 d ≤ λ/2），则无论 m 取何值，都不会有多个解。所有 m > 0 的情形都会导致 arcsin 自变量大于 1。这是唯一能避免在可见天区出现栅瓣的方法。
• 但如果我们有意将 ∆Φ 限制在小于 ±π 的范围内，那么即使 λ/d 较小，也仍可能避免栅瓣的出现。缩小 ∆Φ 的范围意味着限制阵列的最大波束扫描角度。这是一个有趣的权衡问题，我们将在下一节中进一步探讨。

阵元间距的考虑

阵元间距是否应始终小于 λ/2？并不一定！这实际上是天线设计人员需要权衡的因素之一。

如果波束需要完全扫描至地平线方向，那么 θ = ±90°，此时若不允许在可见半球内出现栅瓣，则阵元间距必须为 λ/2。但在实际应用中，最大可实现的扫描角总是小于 90°，这是由于单元因子和其他在大扫描角下引起的性能劣化所导致的。

从图 2 中的 arcsin 函数图可以看出，如果 y 轴（即扫描角 θ）被限制在一个较小的范围内，那么栅瓣只会出现在原本不会使用的扫描角度。对于给定的最大阵元间距 d_max ，这个限制的最大扫描角 θ_max 会是多少？我们之前提到过，我们的目标是保持：

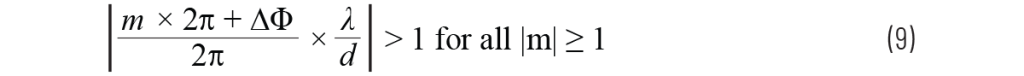
我们可以利用这一点来计算栅瓣（m = ±1）首次出现的位置。将该条件代入，并使用第一部分中公式（1）对 ∆Φ 的定义，得到：

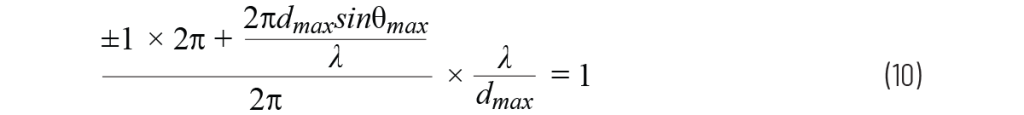
简化为：

然后求解 d_max 得到：

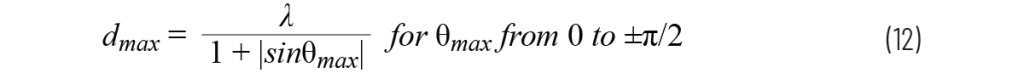
该 d_max  是在限制最大扫描角 θ_max 的条件下不出现栅瓣的最大允许阵元间距（其中θ_max <π/2 ）。

例如，若信号频率为 10 GHz，且希望在 ±50° 扫描范围内不出现栅瓣，则最大阵元间距为：

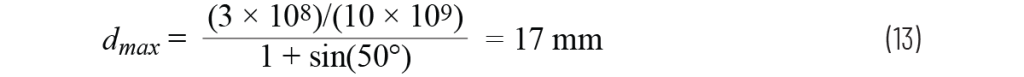
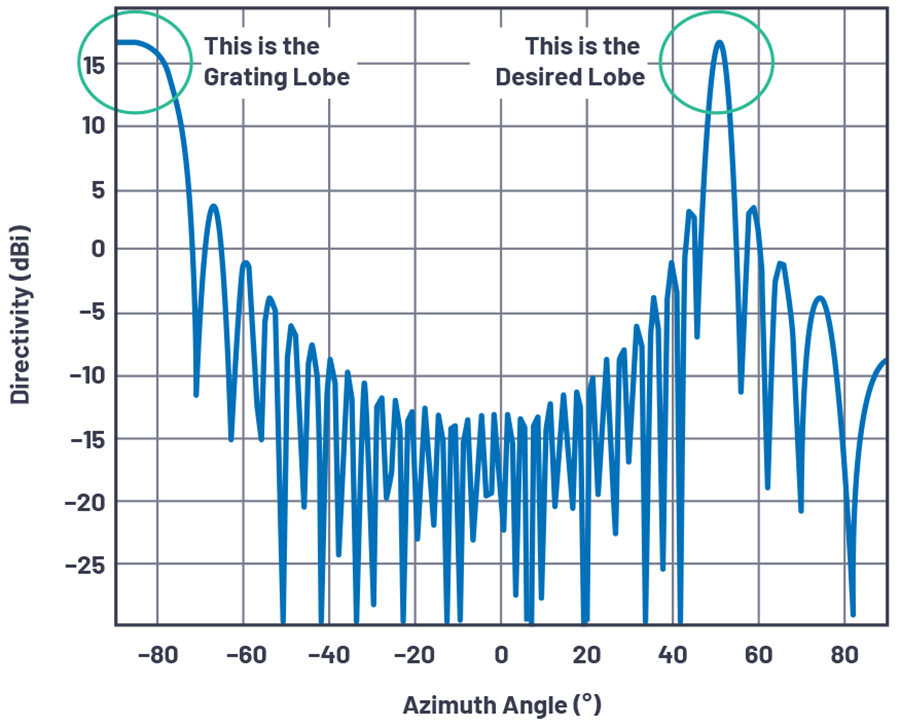
图 4. 当 θ = 50°，N = 32，d = 17 mm，f = 10 GHz 时，在地平线附近开始出现栅瓣。

因此，限制最大扫描角将带来如下自由度：可以增加阵元间距，从而在每通道物理尺寸不变的情况下扩展孔径。例如，对于天线波束始终指向一个较窄预定义方向的应用场景，可以增加单元增益以增强该方向的方向性，同时也可以增加阵元间距以扩大阵列孔径。两者都能在窄波束角内实现更大的整体天线增益。

需注意，即使在零扫描角下，公式（3）也指出最大阵元间距为一个波长，前提是可见半球内不允许出现栅瓣。例如在 GEO 卫星的场景中，整个地球的覆盖角度仅为从机械波束零向偏离 9°。此类情况下，只要栅瓣不落在地球表面上，即可接受其存在。这时，阵元间距甚至可以为多个波长，从而获得更窄的波束宽度。

此外，还有一些值得注意的天线结构试图通过非均匀阵元间距来规避栅瓣问题，这类结构被归类为非周期阵列（aperiodic arrays），例如螺旋阵列（spiral arrays）就是其中一种。出于机械天线结构构建的考虑，可能希望使用可扩展的通用构件模块来构建大规模阵列，但这将形成均匀阵列，从而受到本文所描述的栅瓣条件限制。

波束偏频（Beam Squint）

在第一部分的开头，我们描述了当波前以相对于波束零向的角度 θ 入射到阵列上时，阵元之间会出现时间延迟。对于单一频率的情况，波束指向可以通过将时间延迟替换为相位移来实现。这种方法适用于窄带波形，但对于宽带波形，如果波束指向是通过相位移实现的，那么波束方向将随着频率发生变化。

这可以通过直观方式解释：时间延迟对应于相对于频率的线性相位变化。因此，对于给定的波束方向，所需的相位移会随着频率的变化而改变。或者反过来说，对于一个固定的相位移，波束方向会随着频率而变化。

这种波束方向随频率变化的现象被称为波束偏频（beam squint）。

还需考虑的是，在波束零向（θ = 0）时，阵列中没有任何相位差，因此也就不会产生波束偏频。因此，波束偏频的大小必须是角度 θ与频率变化的函数。

图 5 展示了一个 X 波段的示例。在该示例中，中心频率为 10 GHz，调制带宽为 2 GHz，可以明显看到波束方向随着频率和初始波束角的不同而发生变化。

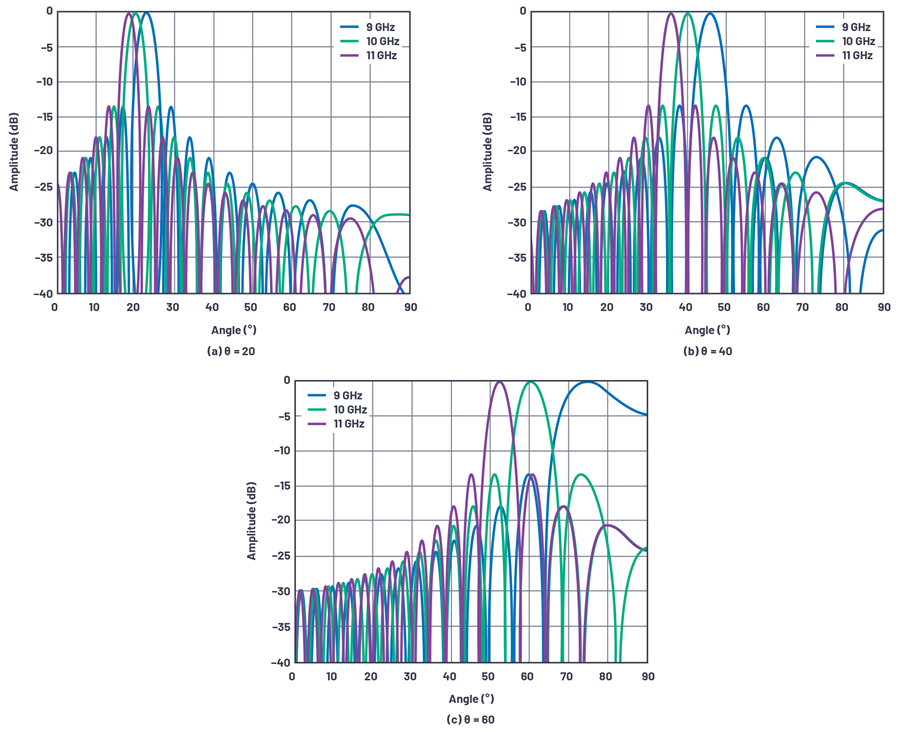
图 5. X 波段中，32 阵元线性阵列（阵元间距为 λ/2）下的波束偏频示例。

波束偏频是可以直接计算的。使用公式（1）与公式（2），可以计算出 波束偏移方向（即波束偏频）如下：

该公式的图示如图 6 所示。图 6 中使用的是f/f₀  的比值形式，这是有意为之。相较于原公式中的 f₀/f ，使用其倒数可更直观地观察频率相对于中心频率的变化对波束方向的影响。

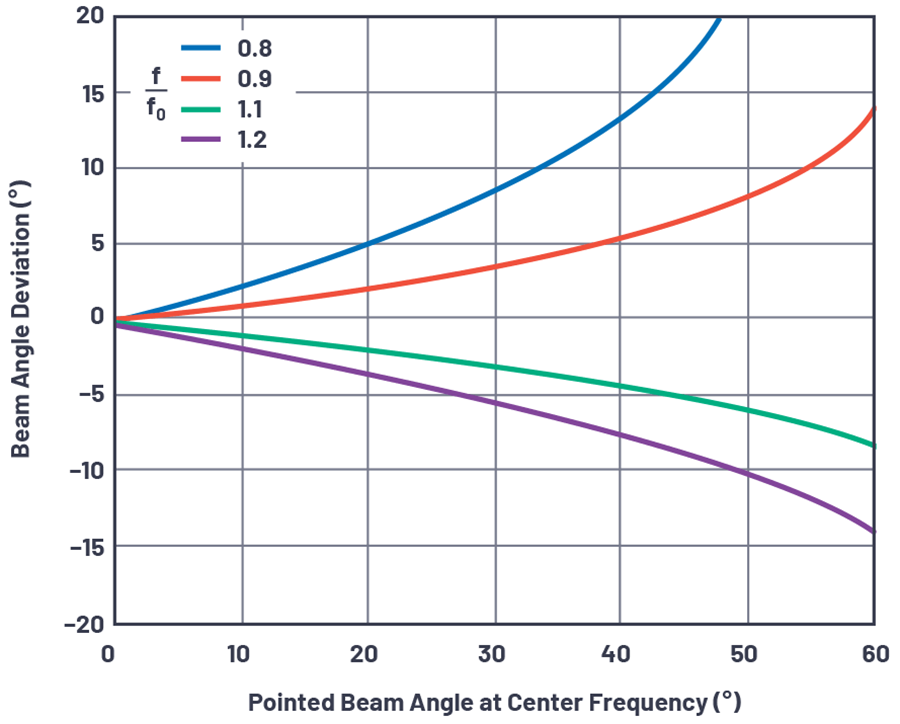
图 6. 不同频率偏移下，波束偏频随波束角的变化关系。

关于波束偏频，有以下几点观察：

• 波束角偏离波束零向越远，频率变化导致的波束偏移越大；
• 低于中心频率的信号引起的波束偏移比高于中心频率的信号更大；
• 低于中心频率的信号使波束进一步远离波束零向。

波束偏频的考量

波束偏频，即波束指向角随频率的偏移，是由于用相位移近似代替时间延迟所引起的。如果采用真实时间延迟单元来实现波束控制，则不会出现这一问题。

既然波束偏频的问题如此明显，为何还要使用相移器而不是时间延迟单元呢？这通常归结于设计的简便性以及相移器相较于时间延迟单元在集成电路（IC）中更易获得。时间延迟通常以某种形式的传输线实现，而所需的总延迟取决于天线孔径的大小。迄今为止，大多数可用的模拟波束形成芯片基于相位移设计，但也已经出现了部分真实时间延迟（true time delay）芯片系列，未来这些芯片在相控阵实现中可能会更加普遍。

在数字波束形成中，可以通过 DSP 逻辑和数字波束形成算法来实现真实时间延迟。因此，在每个阵元都被数字化的相控阵架构中，自然可以解决波束偏频问题，并提供最灵活的可编程性。然而，这种解决方案在功耗、体积和成本方面可能面临挑战。

在混合波束形成中，先对子阵列进行模拟波束控制，然后对整个阵列进行数字波束控制。这种结构在某种程度上可以天然缓解波束偏频问题。波束偏频仅影响子阵列，而子阵列的波束宽度较宽，因此对波束角偏移更具容忍度。因此，只要子阵列的波束偏频在可接受范围内，就可以采用混合波束形成架构，在子阵中使用相移器，并在后端数字波束形成中使用真实时间延迟。

总结

本文是关于相控阵天线方向图三部分系列的第二部分。在第一部分中，我们介绍了波束指向与阵列因子的基本概念；在第二部分中，我们讲解了栅瓣与波束偏频这两种非理想特性。

在第三部分中，我们将讨论如何通过加权（tapering）来降低旁瓣，并进一步说明相移器量化误差所带来的影响。

参考文献

• Balanis, Constantine A. Antenna Theory: Analysis and Design, 第三版，Wiley-Interscience，2005。
• Longbrake, Matthew. True Time Delay Beamsteering for Radar. 2012 IEEE National Aerospace and Electronics Conference (NAECON)，IEEE，2012。
• Mailloux, Robert J. Phased Array Antenna Handbook, 第二版，Artech House，2005。
• O’Donnell, Robert M. “Radar Systems Engineering: Introduction.” IEEE，2012 年 6 月。
• Skolnik, Merrill. Radar Handbook, 第三版，McGraw Hill，2008。