您的购物车目前是空的!
标签: CN0566
-
X波段相控阵雷达开发平台-设备高阶指南
欢迎
欢迎阅读本指南,本指南旨在让想从头开始配置设备的用户阅读,本指南作为一份指导,会帮你解决安装过程中的大部分问题,但是您仍然会遇到各种奇奇怪怪的问题,希望您可以在Google无果后与我们咨询问题。
本指南默认认为您具备Linux使用能力,具备Git等能力。
请自购一张SD卡,请勿使用套件中的SD卡,套件中的SD卡作为保底使用,当您无法完成本指南得时候,还是可以使用随货发出的保底SD卡正常使用。
制作SD卡
SD卡烧录工具:Raspberry Pi Imager

镜像下载地址:image_2023-04-02-ADI-Kuiper-full.zip
在使用的时候,选择设备中,选择树莓派4。
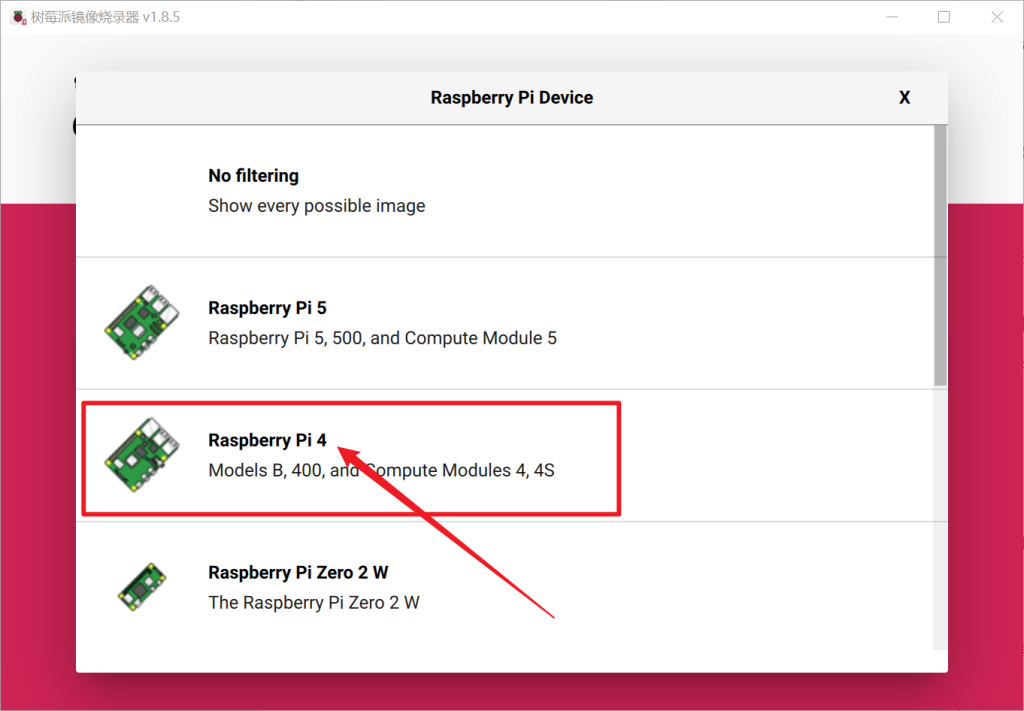
系统镜像请勿选择官方的,而是选择custom
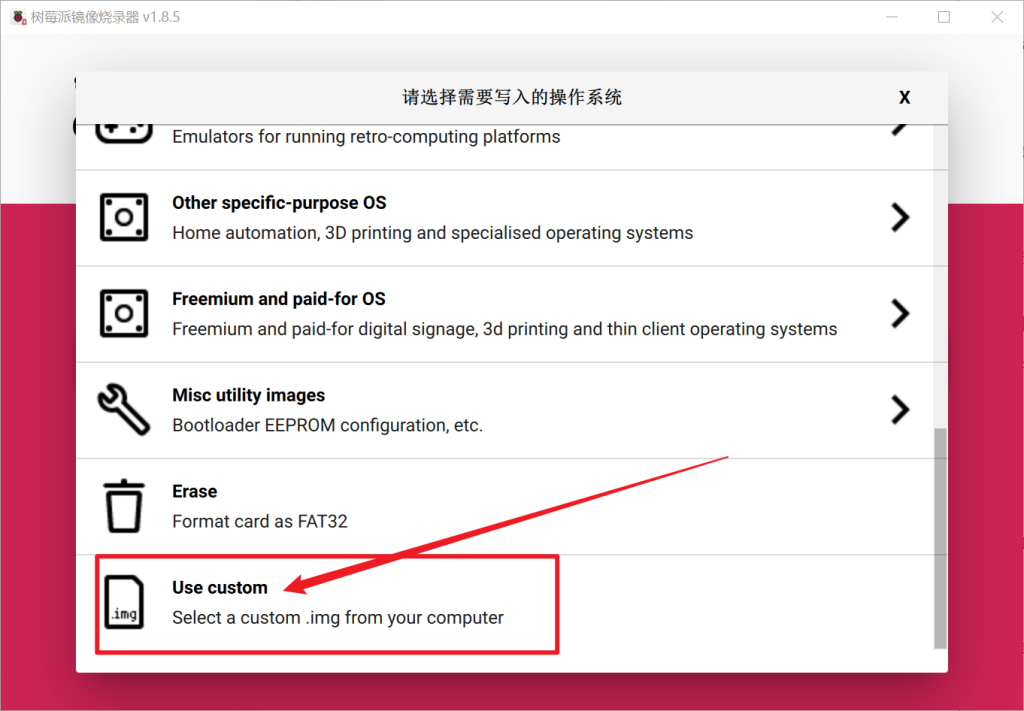
然后选择我们下载的镜像即可。接下来完成烧写之后,即可插入树莓派中,进行开机了。
用户名和密码
用户名和密码,可以用于后续的SSH远程连接。
用户名 密码 root analog analog analog 启用树莓派 VNC 服务
在终端输入以下命令进入配置界面。
sudo raspi-config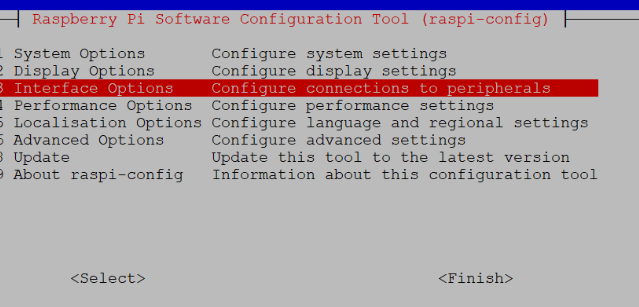
依次操作:Interfacing Options -> VNC -> Yes。之后系统会提示你是否要安装 VNC 服务,输入 y 之后回车,等待系统自动下载安装完成,一切顺利的话 VNC 服务就启动了!
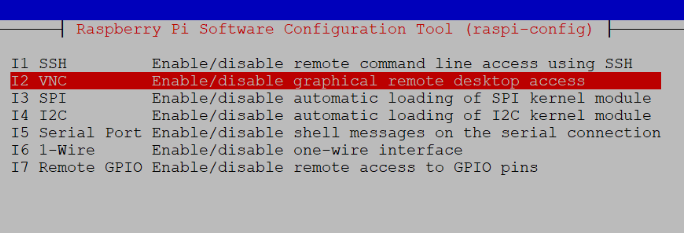
安装NTP 模块
sudo apt-get install ntp使用命令重启ntp服务:
sudo service ntp restart检查当前的时间同步状态:
timedatectl status这个是为了后续的安装软件使用。
配置代理
注意打开局域网连接
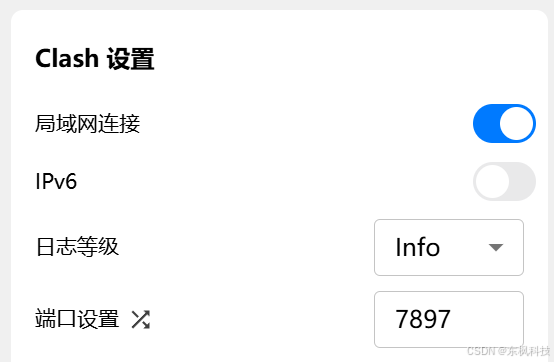
注意记住端口号

查看自己电脑的IP是多少,可以用CMD查看
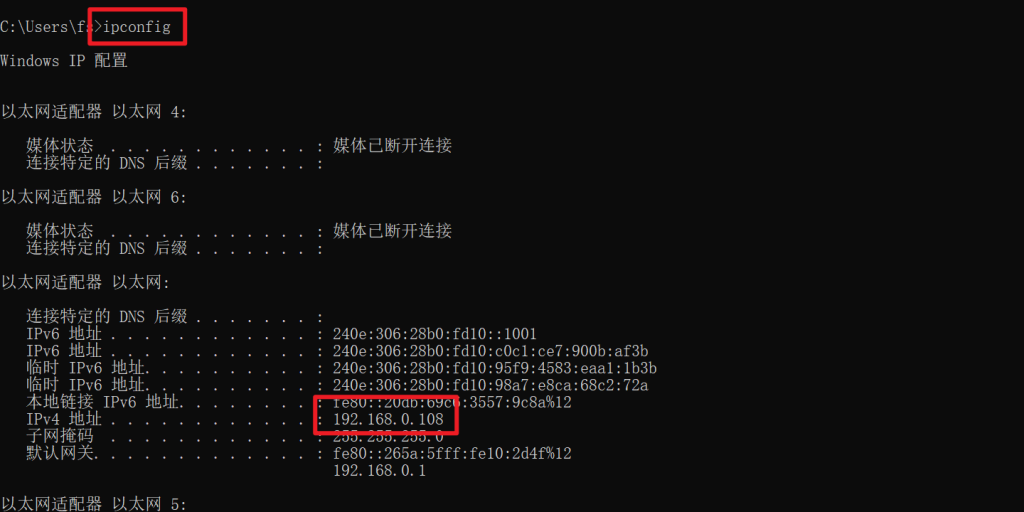
IP地址因机器而不同。
在设备的命令行中输入:
sudo nano /etc/environmentenvirinment内输入(注意下文是模板,你需要根据实际情况进行修改):
export http_proxy="http://username:password@proxyipaddress:proxyport" export https_proxy="http://username:password@proxyipaddress:proxyport" export no_proxy="localhost, 127.0.0.1"用代理的IP地址和端口替换proxyipaddress和proxyport。
export http_proxy="http://192.168.0.108:7899" export https_proxy="http://192.168.0.108:7899" export no_proxy="localhost, 127.0.0.1"保存的话,按下:Ctrl + X
然后在设备的命令行中输入:
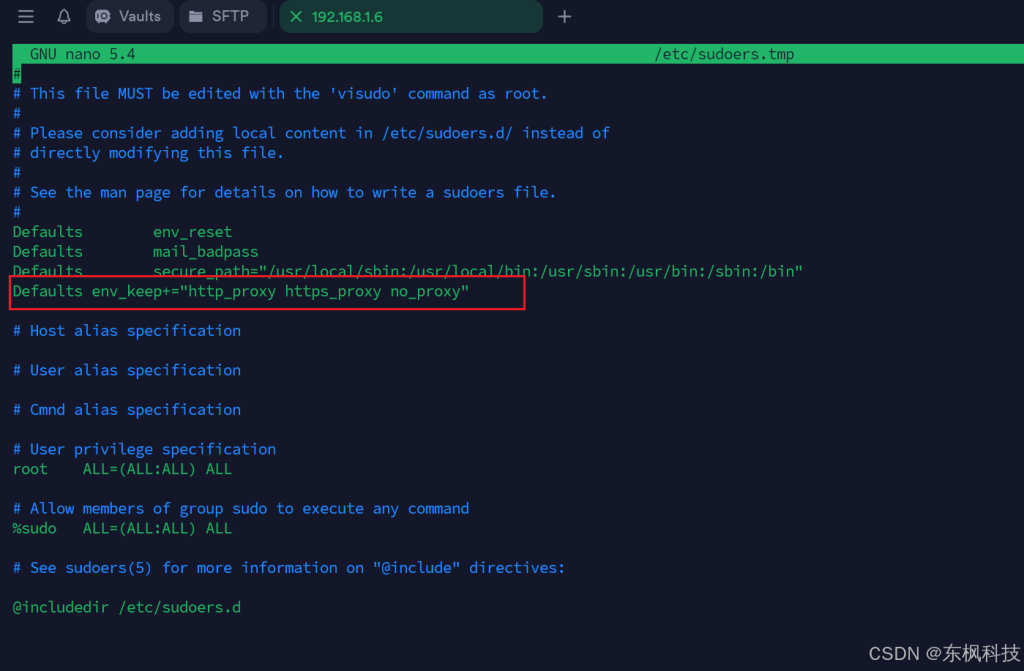
sudo visudo将下面的行添加到文件中,这样sudo将使用您刚刚创建的环境变量(注意查看位置):
Defaults env_keep+="http_proxy https_proxy no_proxy"注意拷贝的位置
重启
sudo reboot安装相控阵相关软件
wget https://github.com/thorenscientific/rpi_setup_stuff/raw/main/phaser/phaser_sdcard_setup.sh sudo chmod +x phaser_sdcard_setup.sh ./phaser_sdcard_setup.sh sudo reboot重启之后运行
sudo pip install --force-reinstall numpy==1.22你可以参考其他的文档进行下一步的实验之旅了!
-
X波段相控阵雷达开发平台-开发指南

欢迎
欢迎您查看本指南,我们将会带您一步一步的进行案例的操作。
请您准备好:
- 带HDMI的显示器
- 有线鼠标和键盘
- Micro-HDMI转HDMI线(东枫包装箱内提供)
连线以及注意事项

- Micro-HDMI 注意要连接到第一个孔位上。
- Type-C电源适配器要连接到相控阵主板上,树莓派请勿上电。
- 网口可以连接网络(支持上网)
- Pluto-SDR连接线是单独配置的短线,方便使用。
- SD卡内已经安装好系统和软件,请勿随意格式化或者重新安装系统,如果您想自己制作系统和安装软件,请重新购置一张32GSD卡,在您自己购置的SD卡上进行操作,我们发货的SD卡不要重新刷系统。
上电开机
终端介绍
设备上电之后,会自动开机,进入系统。当完成开机之后,您可以在显示器上看到这样的界面
在树莓派的系统中,最重要的就是使用命令行终端。

如果熟悉树莓派的都知道,是需要知道用户名和密码的。
用户名 密码 root analog analog analog 当你需要密码的时候,使用上述的信息即可。
设备连接WIFI
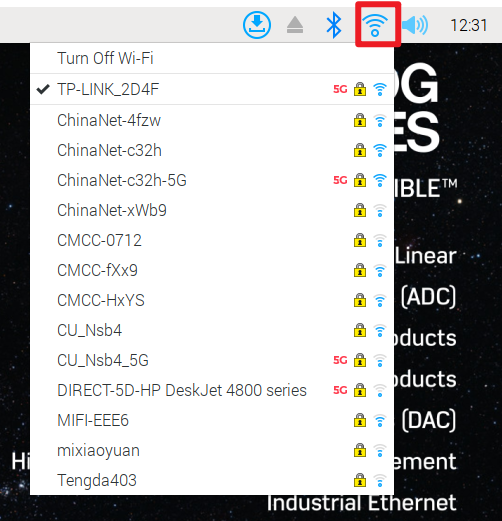
在右上角是可以连接WiFi的,这样就可以无线网线了,低延迟还是网线最稳定,WiFi是使用的树莓派自带的模块。
在Windows上使用使用VNC登录
Windows电脑上需要安装RealVNC Viewer
在设备的终端中输入指令:
ifconfig于是会显示出IP地址。
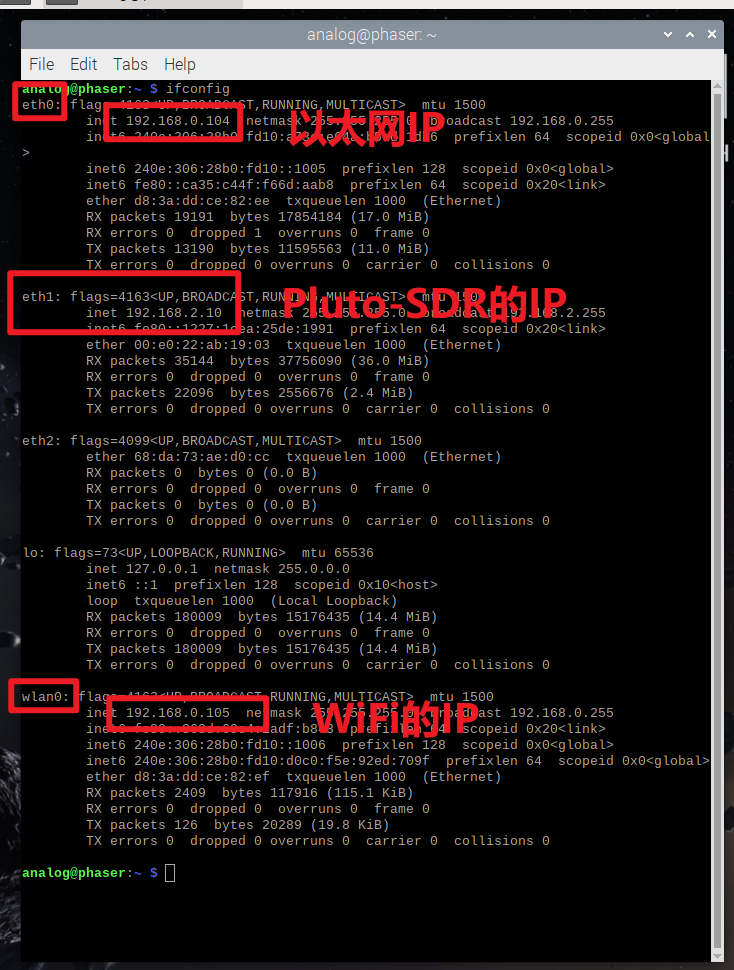
在这个界面中,是可以看到所有的IP地址的
在RealVNC Viewer中输入设备的IP地址,按照提示输入密码即可。
快速访问手册
打开浏览器

然后点击手册
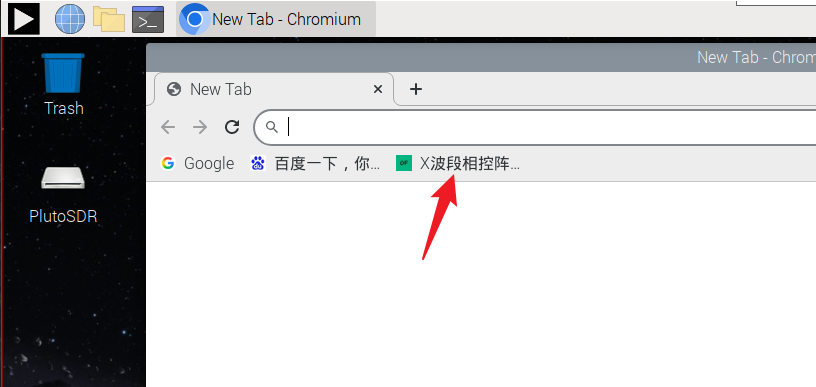
复制和粘贴指令会非常的方便。
在终端中,按下右键,然后选择“Paste”
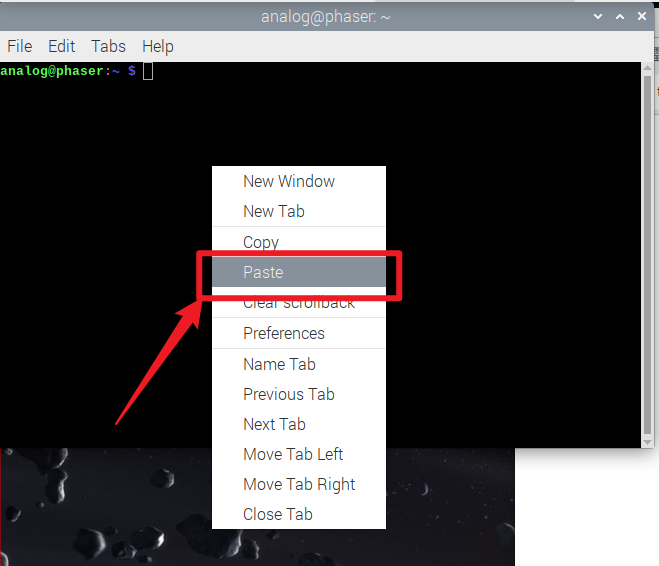
就可以把指令复制过来了。按下键盘的Enter建运行。
实验步骤:查找HB100和相控阵雷达界面
此时,可以从命令行运行GUI 。使用 3V 台式电源或两节 AA 电池为 HB100 源供电,并将其对准移相天线。运行以下命令查找 HB100 频率:
注意:是需要打开终端的,在终端中一行一行的输入,按下回车键运行。
cd ~/pyadi-iio/examples/phaser python phaser_find_hb100.py理想情况下,应该有一个单一的、尖锐的峰值,如下图所示。
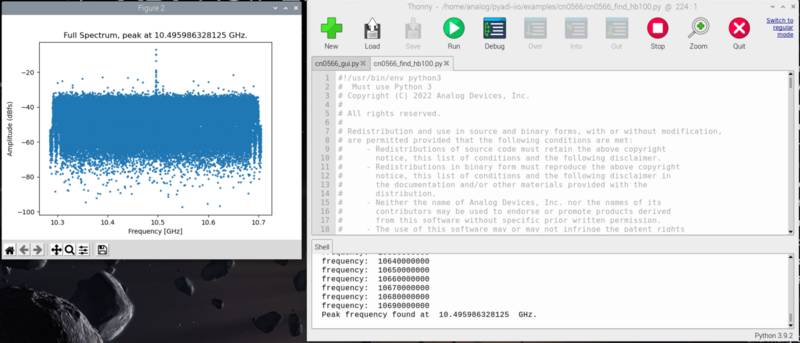
如果只有一个显著峰,输入“y”。如果出现多个峰或没有可见峰,请关闭绘图并在提示符下输入“n”。重新放置 HB100(并确保附近没有其他源),然后重新运行脚本。
接下来运行GUI:
cd ~/pyadi-iio/examples/phaser python phaser_gui.pyGUI应加载并开始显示光束模式,如下所示。
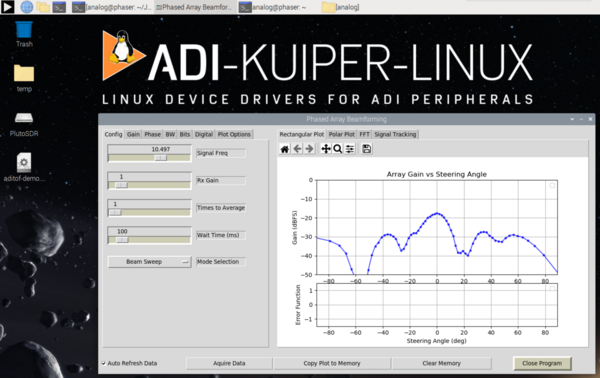
数据的捕获是可以单次捕获或者连续捕获的。
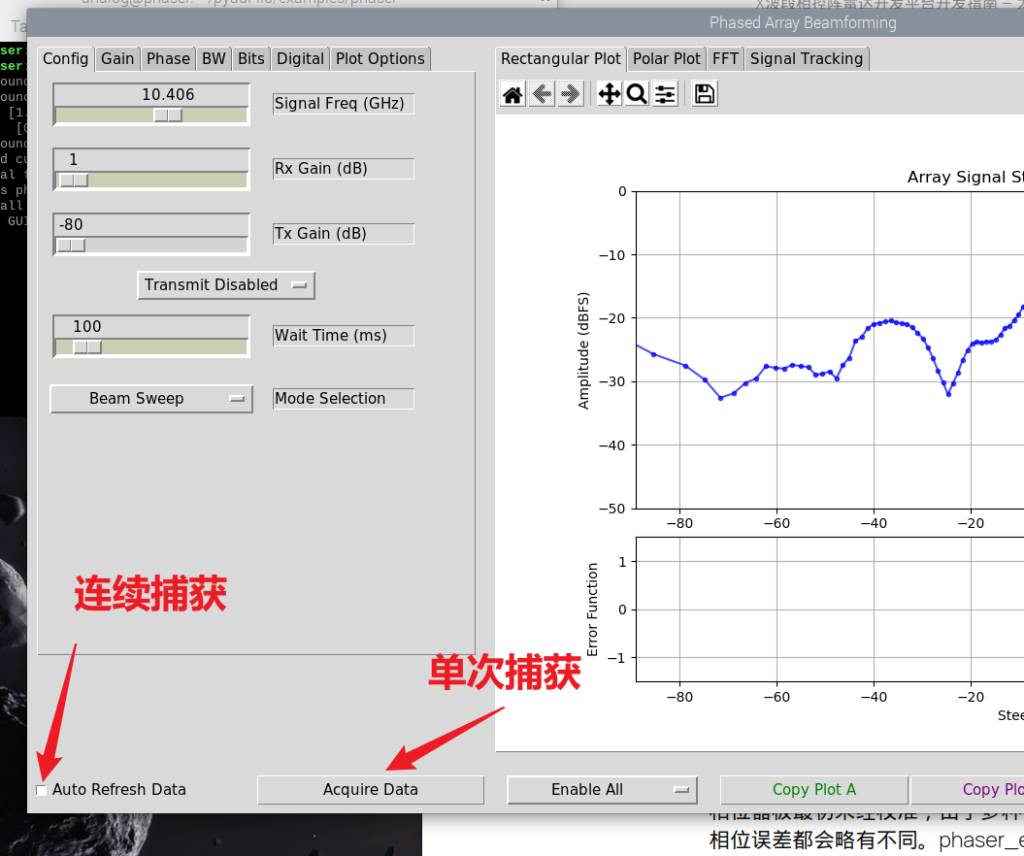
在该案例中,发射源可以是使用外置的HB100,也可以使用设备自己发射的信号。如果使用外置的HB100当作信号源,那么就在界面中选择“Transmit Disabled”,注意HB100要保持开机状态。HB100是电池供电的,在使用完成之后,记得给断电。
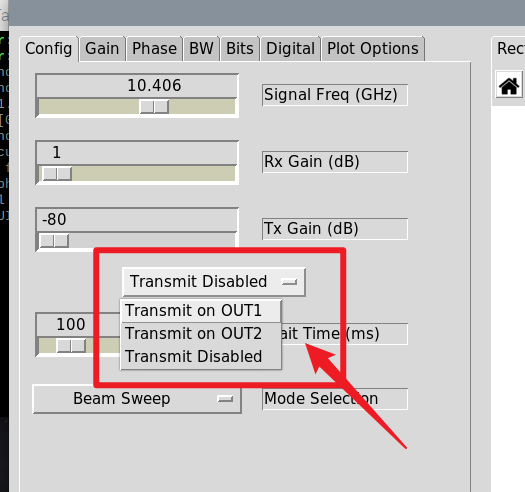
当选择使用设备自身的信号源的时候,请在软件中选择“Transmit on OUT1”或者“Transmit on OUT2”
使用的硬件为:定向天线+SMA转接头+SMA射频线

连接起来之后就是

连接设备的OUT1或者OUT2

默认的“Rectangular Plot”,可以在Plot Options中选择“Show Peak Gain”和“Show Peak Angle”,这样的目的是为了能方便看出辐射源的方位。
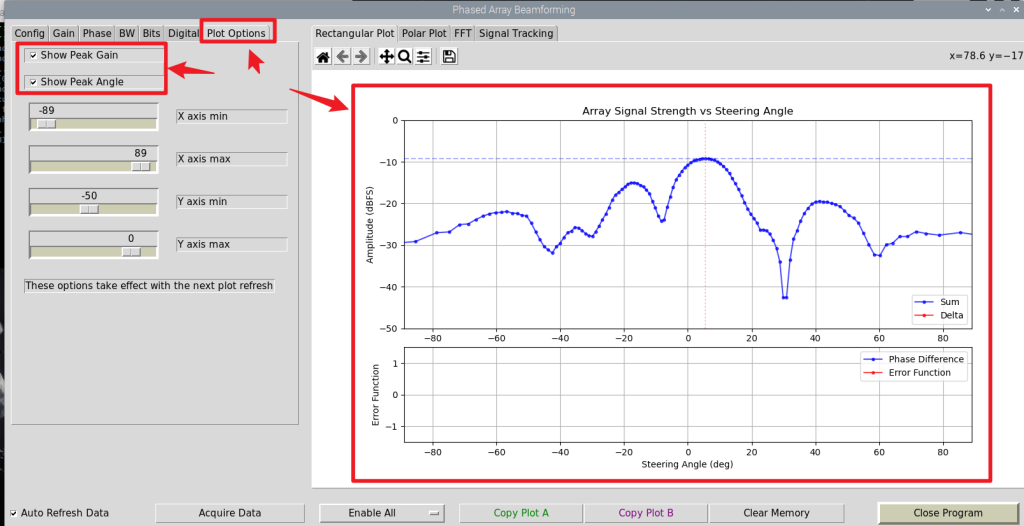
图像的显示不仅有“Rectangular Plot”,还有“Polar Plot”
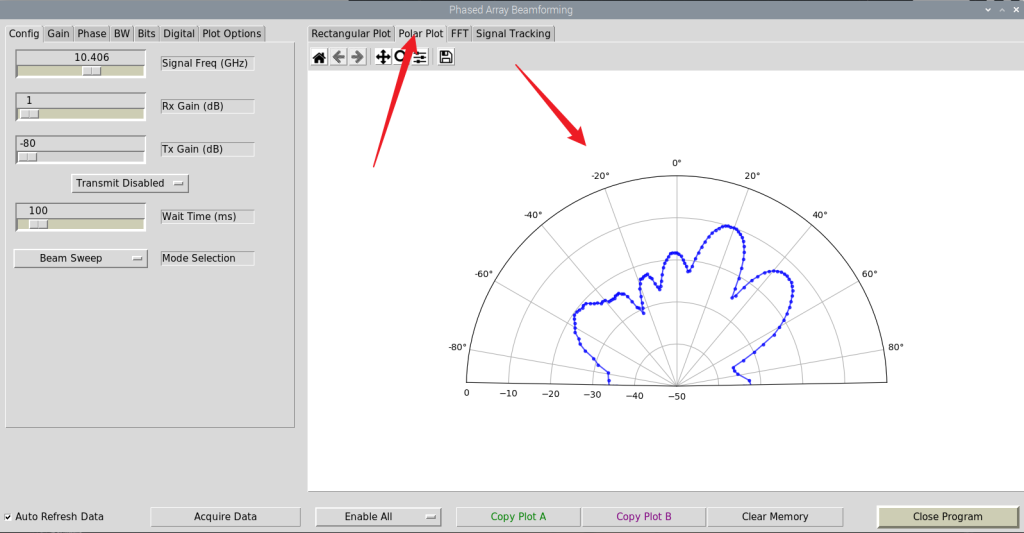
还有“FFT”显示
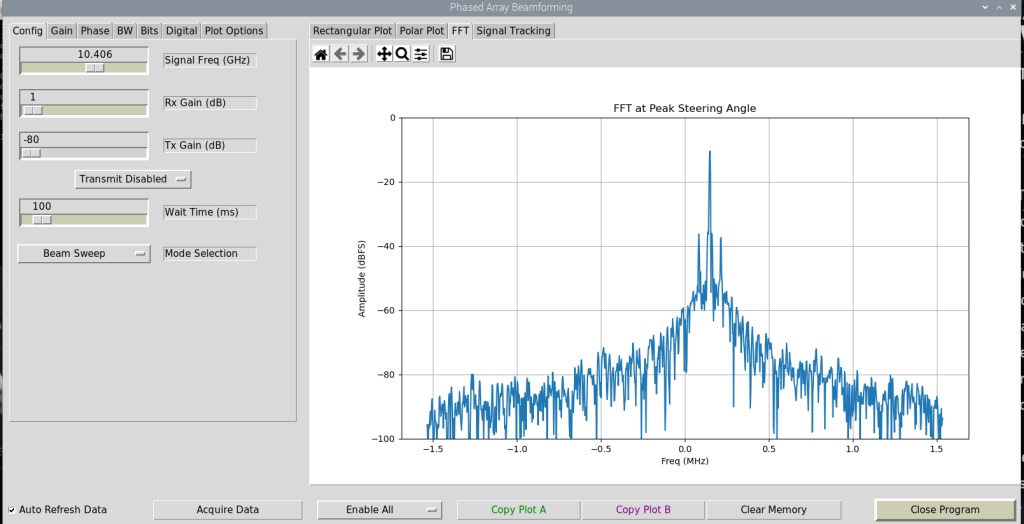
对于相控阵而言,拥有八个通道,这八个通道的增益和相位是可以控制的。在界面中“Gain”和“Phase”是可以去更改这些数值的。
增益(Gain):
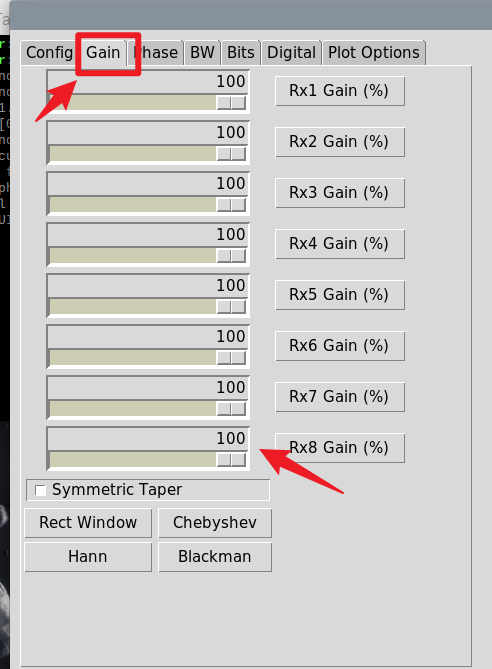
相位(Phase):
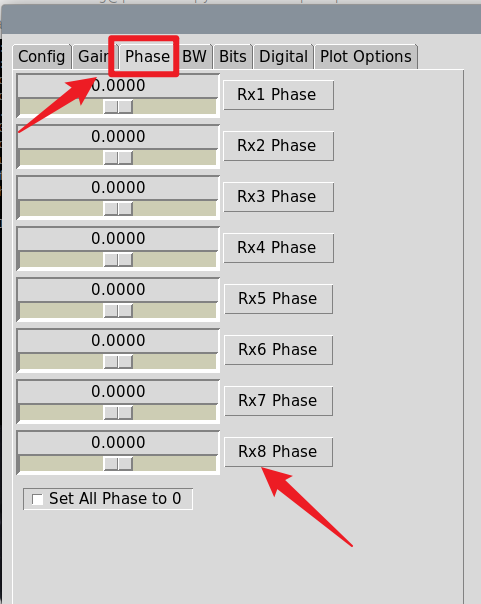
跟踪模式,选择“Tracking”
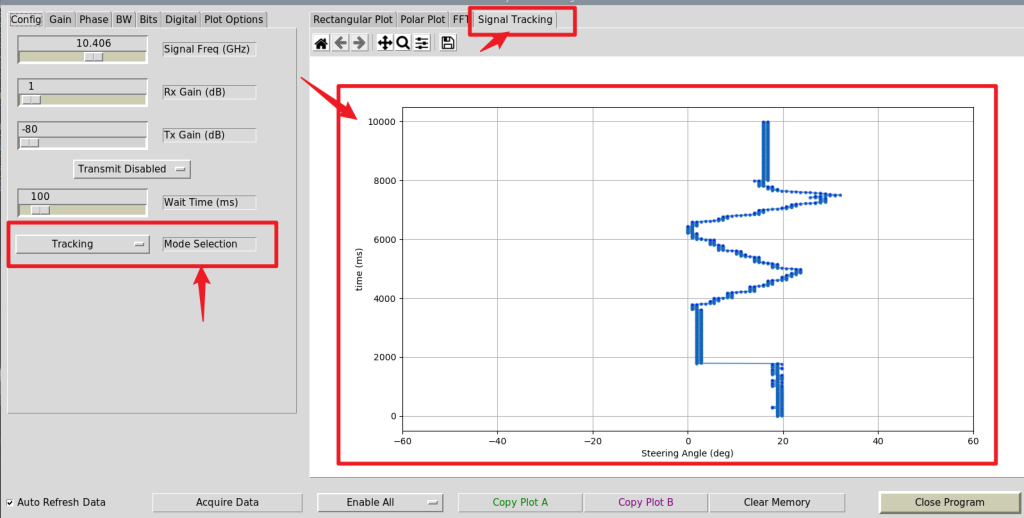
初始校准
相位器板最初未经校准;由于多种因素的影响,每个元件的增益和相位误差都会略有不同。phaser_examples.py 脚本提供了一个校准实用程序,可以生成校准文件。如果 GUI 正在运行,请将其关闭。将 HB100 放置在阵列正前方,机械视轴对准,距离约 1.5 米。然后运行:
cd ~/pyadi-iio/examples/phaser python phaser_examples.py cal该脚本运行时会提供调试信息和绘图,您可能需要关闭每个绘图才能继续运行脚本。运行此脚本后,文件 gain_cal_val.pkl 和 phase_cal_val.pkl 将放置在工作目录中。GUI 程序再次运行时也会自动加载这些文件。