您的购物车目前是空的!
作者: zhao xudong
-
KrakenSDR 天线阵列设置
关于标准测向天线的说明
在标准的无线电测向中,您需要 五根相同的全向天线。虽然可以在性能上妥协,使用较少的天线,但为了获得最佳性能,我们强烈建议使用 全部五根天线。这些天线通常是磁吸式鞭状天线或偶极子天线。
我们建议始终使用 均匀圆形阵列(Uniform Circular Array, UCA) 的布置方式,因为它可以从所有方向获取方位信息。相比之下,线性阵列存在局限性,它无法区分信号是从阵列的正前方还是正后方传来的。
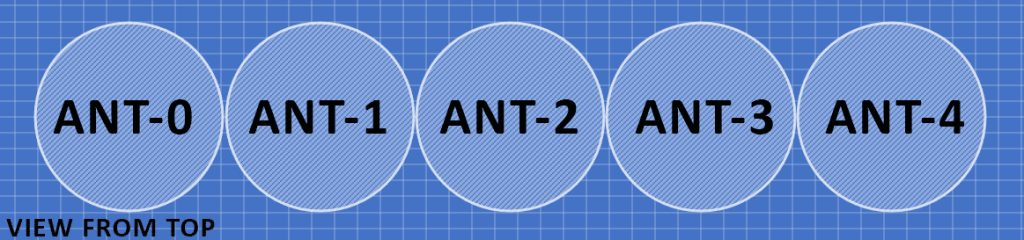
注意,在安装天线时,约定的布置顺序是 从俯视角度看为顺时针方向。也就是说,天线0(antenna zero) 指向 0 度方向,天线1 位于天线0右侧的位置,依此类推。
下方的说明将提供关于如何优化天线阵列的更详细信息。但如果您只是想快速上手,最简单的方式是使用我们提供的 Excel 天线阵列间距计算器文件 Antenna_Array_Size_Calculator.xlsx,
间距倍数说明(Spacing Multiplier Explained)
天线阵列的尺寸由 间距倍数(spacing multiplier) 与信号频率共同决定。间距倍数是一个系数,它乘以所测频率对应的波长,得出天线阵列中各元素之间的 “阵元间距(interelement spacing)”,即相邻天线之间的距离。
在所有应用场景中,间距倍数必须小于 0.5,以避免产生歧义(即出现多个可能的方位解)。
理想情况下,间距倍数应 保持在 0.2 以上并尽量接近 0.5。间距倍数越大,阵列的角分辨率越高,能够更好地处理多径效应。但如果间距倍数低于 0.2,阵列的分辨能力就会显著下降,影响测向精度。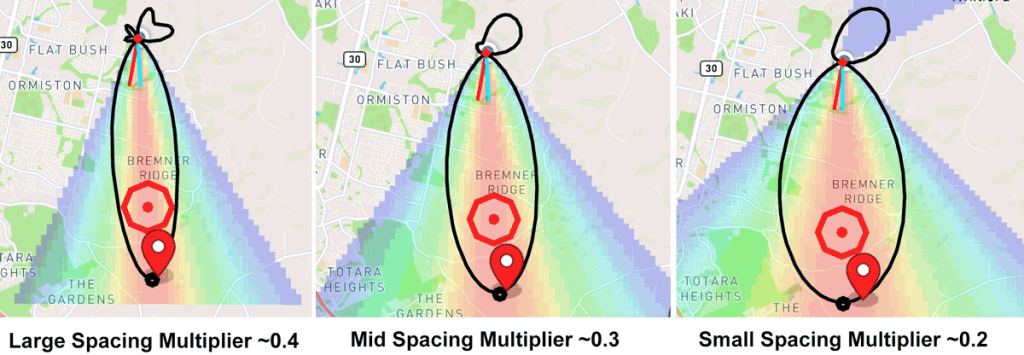
使用 Excel 计算器
在 Excel 计算器中,黄色框表示可以更改的数字。
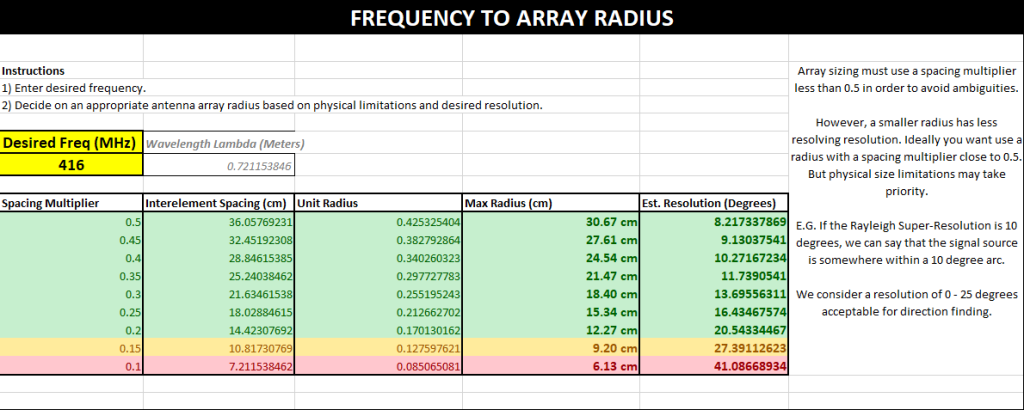
频率转阵列半径
在此处输入您的频率,系统将根据该频率和一系列不同的间距倍数(Spacing Multiplier),为您显示对应的天线阵列半径。
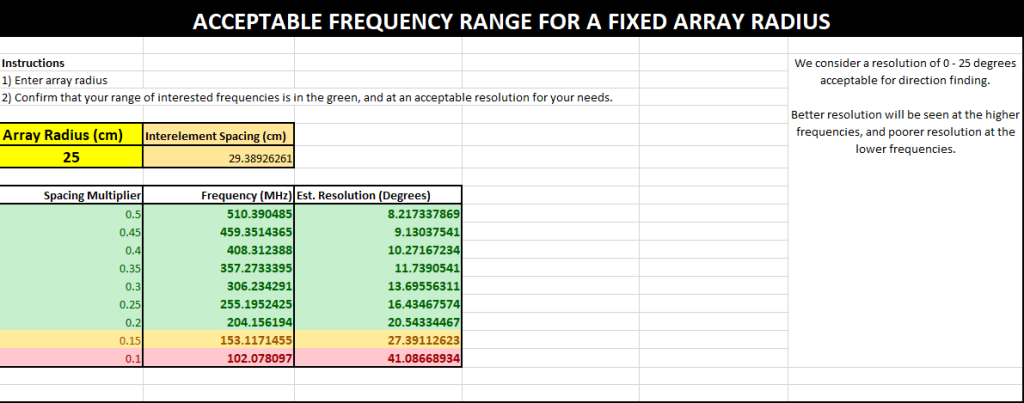
固定阵列半径下的可接受频率范围
一旦您为应用选择了一个合适的阵列半径,请在此处输入该半径。绿色区域将显示在该阵列半径下可正常工作的频率范围。
阵列半径对应的坐标位置
本部分将为您提供在特定阵列半径下,每个天线单元的精确摆放坐标。请注意:这些坐标需要进行旋转,使得 ANT-0(天线0)指向运动方向。
天线间距模板
您可以使用我们提供的天线间距模板,以帮助实现更精确的天线布置。阵列布置越准确,测向结果就越可靠。
用于 3D 打印 和 纸质打印 的模板文件可在以下获取:

对于两种模板,请分别打印中间的五边形和五个臂,然后将它们粘合在一起。

每个孔的间距以 50mm 半径递增,即您可以得到以下阵列半径选项:
- 100mm
- 150mm
- 200mm
- 250mm
这些半径适用于以下频率范围:
- 100mm:510 – 1275 MHz
- 150mm:340 – 850 MHz
- 200mm:255 – 637 MHz
- 250mm:204 – 510 MHz
天线排列方式
均匀圆形阵列(Uniform Circular Array, UCA)
如果您希望从 360 度全方位检测无线电信号源,则天线应布置成均匀圆形阵列(UCA)。阵列中的阵元间距(即相邻天线之间的顶点距离)必须根据目标频率范围进行精确设计。
您必须确保设计的阵列满足以下条件:

若阵列的阵元间距超过该上限,将出现所谓的**“歧义”现象**。简单来说,系统可能会检测到多个可能的信号方向,而无法判断哪一个才是真实的方向。这会严重影响测向精度,因此务必将 spacing multiplier 保持在 0.5 以下。
在实际应用中,为了缩小阵列尺寸,可以适当降低 spacing multiplier,代价是测向精度的下降。通常 最低可以接受到 s = 0.2,我们推荐的典型设置是 s = 0.33。需要注意的是,spacing multiplier 越小,阵列的方向分辨率越低,尤其对于 5 元阵列而言,当 s 低于约 0.2 时,测向精度会变得不可接受。
由于阵元间距与波长直接相关,因此频率越低,波长越长,所需阵列尺寸就越大。这意味着在低频(如 HF 和部分 VHF 频段)下,使用该类型的方向测量方法可能不太现实,因为阵列会占用很大空间。在这种情况下,更适合使用如 TDoA(到达时间差)、Watson-Watt 或 手动八木天线 等其他测向方法。
使用阵列半径而非阵元间距进行布置
有时使用阵列半径来构建圆形阵列比直接测量阵元间距更方便。对应的计算公式为:

这个公式可帮助您根据目标频率设计出适当的天线布置半径。
均匀线性阵列(Uniform Linear Array, ULA)
另一种天线阵列的布置方式是 均匀线性阵列(ULA),即将天线沿一条直线等间距排列。这种方式的缺点是阵列仅对 180 度范围内的信号有效,无法判断信号是从阵列前方还是后方到来。
ULA 的优点在于,它可以提供更高的角分辨率精度,这是因为在相同波长条件下,它允许构建更大的有效孔径。但这种更高的分辨率仅对从接近垂直方向射入的信号有效。当信号角度接近 0 度或 180 度时,天线阵列“看见”的有效孔径显著减小,从而降低了测向精度。
你可以这样理解:当信号从阵列边缘方向到达时,阵列“看到”的有效接收面积远小于信号垂直入射时。因此,线性阵列仅适用于已知信号大致方向,且其不会偏离太多的特定应用场景。
阵元间距计算(与 UCA 相同)
线性阵列的阵元间距计算公式与 UCA 相同:

天线与同轴电缆的精度要求
KrakenSDR 不会对外部天线系统引入的相位失真进行补偿,因此您必须使用完全相同的天线和完全相同长度的同轴电缆,并尽可能精确地布置天线阵列。我们建议使用 KrakenSDR 提供的阵列间距模板来辅助安装。一个实用建议是:在天线安装完成后,实际测量阵元间距,确认所有天线之间的距离完全一致。
在频率不超过约 900 MHz 的情况下,连接 KrakenSDR 的同轴电缆必须长度一致,公差应控制在 1 厘米以内。如果电缆长度存在差异,将会导致测向失败。
您所使用的频率越高,对天线位置精度和电缆长度一致性的要求就越严格。例如:
- 在 800 MHz 时,1 cm 的电缆长度差异可导致阵列各天线之间出现 高达 14 度 的相位失真;
- 在 400 MHz 时,同样的 1 cm 差异会产生约 7 度 的相位失真。
需要注意的是,这种相位失真仅发生在天线阵元之间,并不会直接等同于测向角度的误差,但它仍会对系统测向性能产生显著影响。
因此,在搭建天线阵列时,保持电缆长度的一致性和布局的对称性至关重要。
天线阵列布置建议
车载应用
在车辆上进行测向时,天线阵列应安装在车顶,尽可能远离任何可能阻挡信号的物体。理想情况下,应移除如行李架等可能遮挡天线的部件,以减少干扰。
固定站点
在固定站点部署时,应尽量将天线阵列安装在尽可能高的位置,远离障碍物。附近的障碍物(如其他天线、铁杆、屋顶等)可能引起多径效应或信号折射,从而扭曲信号的入射角度,导致测向结果不准确。
同轴电缆布线建议
无论是车载还是固定站点,同轴电缆应布置整齐,尽可能朝同一方向敷设,并使用扎带捆绑在一起。这种规范的布线方式可确保所有电缆在弯曲时产生的相位失真保持一致,从而减小误差。
多阵列干扰问题
有些固定阵列(如 Arrow Antennas 提供的阵列)设计了可供不同半径使用的多个天线孔位。请注意:一次只能使用一组指定的天线元素。如果同时安装了多个(未使用的)天线元件,这些多余元件会对信号产生阻挡、反射和折射,从而严重扭曲系统对信号方向的判断结果。
多阵列系统的部署建议
如果必须同时部署多个天线阵列,应采用以下两种方式之一以避免相互干扰:
- 水平分隔:将多个阵列相距较远水平布置;
- 垂直分层:例如将小型阵列堆叠在大型阵列上方,以充分拉开空间距离。
正确的天线布置和空间隔离是确保测向系统性能的关键。
伸缩天线长度说明
以下是我们 KrakenTenna 天线套装的可用频率范围。这些天线为相对宽带设计,其工作特性并不完全等同于传统的 1/4 波长接地天线。
注意:我们从最底部(最粗)的段开始计量。
最细、最顶部的那段是第 7 段,最粗、最底部的是第 1 段。这些频率范围是基于在**金属接地面(例如车顶)**上放置天线时的 SWR(驻波比)测量结果得出的。若没有合适的接地面,性能和频率响应可能会有所不同。
如果您使用的频率没有出现在下表中,请选择与该频率最接近的段数进行伸展。例如:
- 对于 161 MHz,可选择 拉出三段天线使用。
这种方式可大致匹配天线长度与频率,实现较优的驻波比表现。
扩展 频率范围 (MHz) 0 440 – 1050 1 366 – 950 2 330 – 1000 3 145 – 158, 290 – 420, 612 – 1050 4 140 – 156, 270 – 360, 595 – 1030 5 135 – 155, 250 – 330, 520 – 1050 6 130 – 150, 240 – 290, 460 – 1050 7 127 – 150, 235 – 282, 450 – 1050 外部射频组件注意事项
请注意,任何置于射频链路中的外部组件(如开关、LNA 放大器、滤波器等)都可能对天线信号产生相位失真,从而导致测向结果不准确。
建议在使用前进行实验室测试,以确认所使用的组件是否会引入不可忽略的相位偏差。
一般来说:
- 普通滤波器通常引起的相位失真可以忽略不计;
- LNA(低噪声放大器)只要每个通道使用的型号完全一致,且使用了相同的连接器和适配器,通常仅会带来轻微的失真。
在测向系统中,确保 每一路天线通道使用的射频组件完全一致 是保证系统性能的关键之一。
天线选择
如前所述,您最有可能选择使用磁吸式鞭状天线或偶极子天线。
- 磁吸式鞭状天线非常适用于车辆环境。
- 在选择天线时,请确保其具备良好的接地性能,即具有直接接地或电容耦合的接地平面连接,以获得最佳性能。
许多廉价的磁吸天线底座存在接地不良,甚至完全没有接地连接,会严重影响测向效果。
此外,正如上文所述,如果天线的同轴电缆是固定连接在天线底座上的,也需要特别关注电缆长度的一致性容差,以避免因长度不一致引起的相位误差。
KrakenSDR 测向天线套装
如果您订购了 KrakenSDR 的 5 根天线套装,则需要进行简单的组装。操作步骤如下:
- 将 SMA T 型连接器 拧到天线底座上;
- 再将 伸缩鞭状天线 拧到 T 型连接器上;
- 最后连接附带的同轴电缆。
接下来,您需要根据目标频率调整鞭状天线的长度。
在正常情况下,鞭状天线的长度应设为目标频率波长的 四分之一,以获得最佳接收效果。当然,如果您是在车辆上安装天线,出于安全考虑,不建议将天线拉得过长。在大多数情况下,即使鞭长略短于理想长度,系统性能也依然可以接受。
分辨精度理论
如果某个系统的分辨精度为 10 度,那么我们可以理解为:实际的信号方向落在一个 10 度宽的扇形范围内。
下面我们简要说明一个五单元阵列系统在理想条件下可能达到的角度分辨率的理论基础。理论精度估算
- 对于一个 5 元圆形阵列,当阵元间距为 0.5λ 时,理论上可以获得约 8 度 的分辨率;
- 对于一个 5 元线性阵列,在同样的 0.5λ 间距下,理论分辨率可达到 约 3.4 度。
注意:以上是最理想条件下的分辨率,并不考虑多径等外部干扰。在实际测向中,由于来自多个地点的读数可以相互平均,所以小范围的误差通常可以被消除,几乎不会影响整体定位效果。
使用 Rayleigh 公式计算分辨率
我们采用物理学中的 Rayleigh 分辨率公式 来估算误差:

圆形阵列计算示例(n=5,s=0.5):

线性阵列计算示例(n=5,s=0.5):
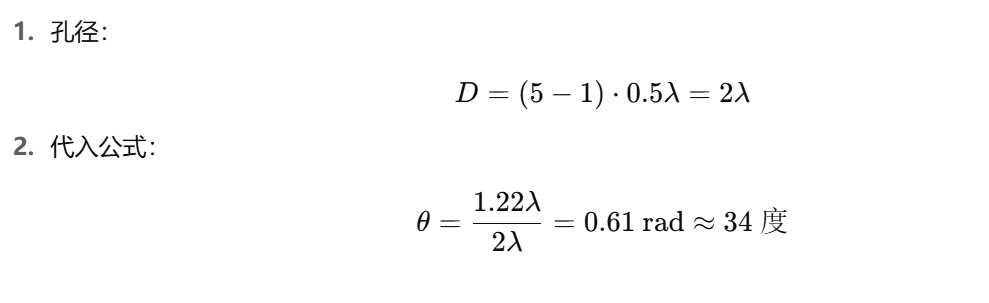
使用超分辨率算法(如 MUSIC)
由于 KrakenSDR 使用了类似 MUSIC(多信号分类) 的超分辨率算法,可将 Rayleigh 分辨率大约提高一个数量级(×10):
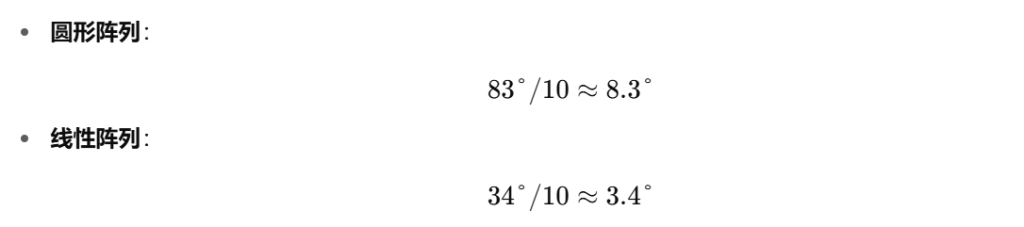
结论:在使用 5 元阵列、0.5λ 间距、并结合 MUSIC 等超分辨率算法的前提下,KrakenSDR 系统可实现约 8.3°(圆形) 或 3.4°(线性) 的方向分辨率。
相关文章
-
KrakenSDR测向背景理论
测向背景
在无线电测向操作中,目标是确定某个射频(RF)发射源的精确位置。该发射源可能是非法或干扰性的发射器,也可能是狐狸猎捕比赛中的信标、资产/宠物/野生动物跟踪信标、搜救信标,或只是一个不明的可疑信号。
要通过三边测量法定位发射源,需要使用无线电测向设备从多个位置测定指向发射源的方位角。然后将这些方位角绘制在地图上,它们的交汇点即为对发射源位置的估计。
然而,无线电测向的方位角通常会存在几度的误差,并且由于“多径效应”(multipath)的存在,测向结果往往会受到较大影响,导致精度下降。
测向方法
1. 基于定向天线的方法:
这些方法使用如八木天线(Yagi)等定向天线,由用户手动旋转天线,寻找信号功率最强的方向,并记录该方向。然后在其他位置重复这一过程,直到能够通过三角测量定位发射器的位置。一些更自动化的方法可能会使用环形排列的多个定向天线阵列来实现。
2. 拟多普勒(Pseudo-Doppler)方法:
拟多普勒方法使用固定的天线阵列,阵列中的每个天线单元会以极短时间轮流依次激活,这模拟了一个天线以极高速度在水平面上旋转的效果。当天线“旋转”朝向信号源时,接收到的频率会升高;当“旋转”背离信号源时,频率则会降低。通过分析这些频率变化,可以确定信号的方向。LoJack 系统(用于警方追踪被盗车辆)就使用了这种较早期的拟多普勒测向技术。业余无线电领域中有多种拟多普勒设备,如使用普通扫描接收机的 RDF42 和 DDF2020T。开源项目 Opera Cake 也为 HackRF 提供了拟多普勒实现。
3. 到达时间差(TDoA, Time Difference of Arrival):
TDoA 方法需要多个时间同步的无线电设备分布在一定距离范围内。每个设备记录接收到信号的时间差,然后利用这些时间差计算接收器之间的双曲线轨迹,进而定位信号源。这种方法是 KiwiSDR 所采用的。4. 相关干涉测向(Correlative Interferometry):
该方法通过提取天线阵列中接收到信号之间的相位差来判断方向。KrakenSDR 就是采用这一测向方法的典型代表。多径效应(Multipath)
多径效应是指目标信号在传播过程中被地形、建筑物或车辆等物体反射或折射,导致无线电测向系统将反射信号误认为是原始信号源。这种情况会使测得的方位角偏离实际方向,甚至可能产生完全错误的读数。最严重的情况是,当接收天线阵列无法与信号源形成视距(Line-of-Sight, LOS)路径时,系统只能接收到反射信号。
一个类比的例子是:你可能在室内看到墙面上的阳光。如果你看不到太阳本身,又不了解光的传播原理,可能会误以为光源是墙壁、镜子或者窗户,而不是太阳。
因此,如果我们在一个多径效应显著的位置(通常是由于缺乏视距路径)进行单点测向,就可能对信号来源方向做出错误判断。为了获得更准确的位置,我们需要在多个地点进行多次测向,借此平均掉那些由于多径效应而产生的偏差读数。
实现这一目标的方式包括:
- 在多个地点部署测向站点,每个站点配备 KrakenSDR 和天线阵列;
- 或者使用单个 KrakenSDR 搭载于车辆中移动,并在多个位置进行测量采样。
此外,使用更大的天线阵列(前提是阵列元间距仍小于半波长)也有助于减轻多径效应的影响。较小的阵列分辨率较低,容易将多径信号混入主瓣,从而导致测向结果偏差;而较大的阵列具有更高的分辨率,多径信号更可能以独立、且较弱的旁瓣形式出现,从而更容易识别和忽略。
移动车载测向理论
许多简单的无线电测向系统需要用户驾驶车辆前往不同地点,手动进行测向并将方位角绘制在地图上。
在 KrakenSDR 系统中,我们利用了现代智能手机的技术,如地图服务、GPS 和指南针传感器。随着车辆移动,系统会自动记录 KrakenSDR 生成的方位角,并结合智能手机传感器提供的当前位置和朝向信息,采集数百次测向读数。随着时间积累,系统会通过计算这些方位角的平均交点,逐步定位发射源的位置。我们使用 MapBox 地图服务将这些数据可视化显示在地图上,方便用户理解,并且还内置了逐步导航功能,帮助用户无需查看地图也能直接前往信号源位置。
高级功能: KrakenSDR 应用实际上使用了一种比简单方位交点计算更智能的方法。它利用了相关干涉测向算法提供的完整 360 度方向数据,这其中也包含了多径信号的方向信息。应用将这些 360 度方向数据叠加在一个网格上,并按一定权重激活对应的网格单元。随着采样次数增加,激活次数最多的网格单元就被判定为包含发射源的位置。
相关文章